当亲本之一未知时,且物种可以自交,则需要在遗传评估中考虑自交的可能性。例如,对于桉树,假设自交概率为0.3是很普遍的。如果不考虑自交,则加性遗传方差将会被高估,因为子代并不都是半同胞——它们越密切相关,因此比模型假定的更相似。
孟德尔抽样是由子代中亲本基因的随机分离与重组所产生的结果。自交会影响矩阵A的对角元素,它代表个体与其自身的共祖率的两倍。自交一代个体的近交系数为0.5。对于反复自交t代,近交系数将会增加到:
$$ F=1-(0.5)^{t} $$
当t很大时,则F将接近于1。
个体与其自身的共祖率为:
$$ \theta_{ii}=0.5*(1+F_i) $$
加性遗传相关矩阵A的对角元素是共祖率的两倍,因此A矩阵对角元素是:
$$ A_{ii}=2\theta_{ii}=1+F_i $$
在ASReml-R中,可以使用参数self来设定自交率s,其中s概率从0到1。下述示例中,将设定不同自交率s,运行相同的模型来演示自交率对遗传评估的影响。
(1.0) 所需程序包
1
2
3
|
library(asreml)
library(AAfun)
library(ggplot2)
|
(2.0) 示例数据集
1
2
3
4
5
6
7
8
9
10
11
12
13
|
df<-asreml.read.table('Pine_provenance.csv',header=T,sep=',')
str(df)
## 'data.frame': 914 obs. of 9 variables:
## $ Treeid : Factor w/ 914 levels "1001","1002",..: 1 2 3 4 5 6 7 8 ...
## $ Female : Factor w/ 36 levels "170","191","192",..: 1 1 1 1 1 1 1 ...
## $ Male : Factor w/ 1 level "0": 1 1 1 1 1 1 1 1 1 1 ...
## $ Prov : Factor w/ 4 levels "10","11","12",..: 1 1 1 1 1 1 1 1 ...
## $ Block : Factor w/ 5 levels "1","2","3","4",..: 1 1 1 2 2 2 2 2 ...
## $ Plot : Factor w/ 180 levels "1","2","3","4",..: 3 3 3 60 60 60...
## $ height : num 12.5 9 10.7 11.6 10.6 10.7 11.5 11.3 10.6 12.8 ...
## $ diameter: num 19.6 11.2 17.8 17.4 17.5 18.6 18.8 16.8 19.2 ...
## $ volume : num 0.1441 0.0339 0.1017 0.1054 0.0974 ...
|
(3.0) 模型分析
(3.1) 常规个体模型
按照传统方法,常规个体模型的分析代码如下:
1
2
3
4
5
6
7
|
ped<-df[,1:3] # pedigree
pedinv<-asreml.Ainverse(ped)$ginv
tm.asr<-asreml(height~Prov,random=~Block+ped(Treeid),
ginverse=list(Treeid=pedinv),
data=df)
|
常规个体模型的方差估计结果如下:
1
2
3
4
5
|
summary(tm.asr)$varcomp
## gamma component std.error z.ratio constraint
## Block!Block.var 0.05371637 0.1083899 0.08719992 1.243004 Positive
## ped(Treeid)!ped 0.44287864 0.8936488 0.32977222 2.709897 Positive
## R!variance 1.00000000 2.0178186 0.28561729 7.064763 Positive
|
(3.2) 自交个体模型
先假定自交率为0.1,则分析代码如下:
1
2
|
pedinv1<-asreml.Ainverse(ped,selfing=.1)$ginv
stm.asr<-update(tm.asr, ginverse=list(Treeid=pedinv1))
|
自交个体模型的方差估计结果如下:
1
2
3
4
5
|
summary(stm.asr)$varcomp
## gamma component std.error z.ratio constraint
## Block!Block.var 0.05074464 0.1083899 0.08719992 1.243004 Positive
## ped(Treeid)!ped 0.34576647 0.7385527 0.27253902 2.709897 Positive
## R!variance 1.00000000 2.1359870 0.24743808 8.632410 Positive
|
通过常规模型和自交模型的比较,会发现Block方差并未发生变化,但加性方差ped(Treeid)和误差方差R均发生变化。加入自交率后,加性方差由之前的0.894下降到0.739,而误差方差则正好相反,从2.018提高到2.136。
(3.3) 不同自交率的影响
同理可以设置不同水平的自交率。不同水平自交的方差分量的估计结果如下:
1
2
3
4
5
6
7
8
9
10
11
12
|
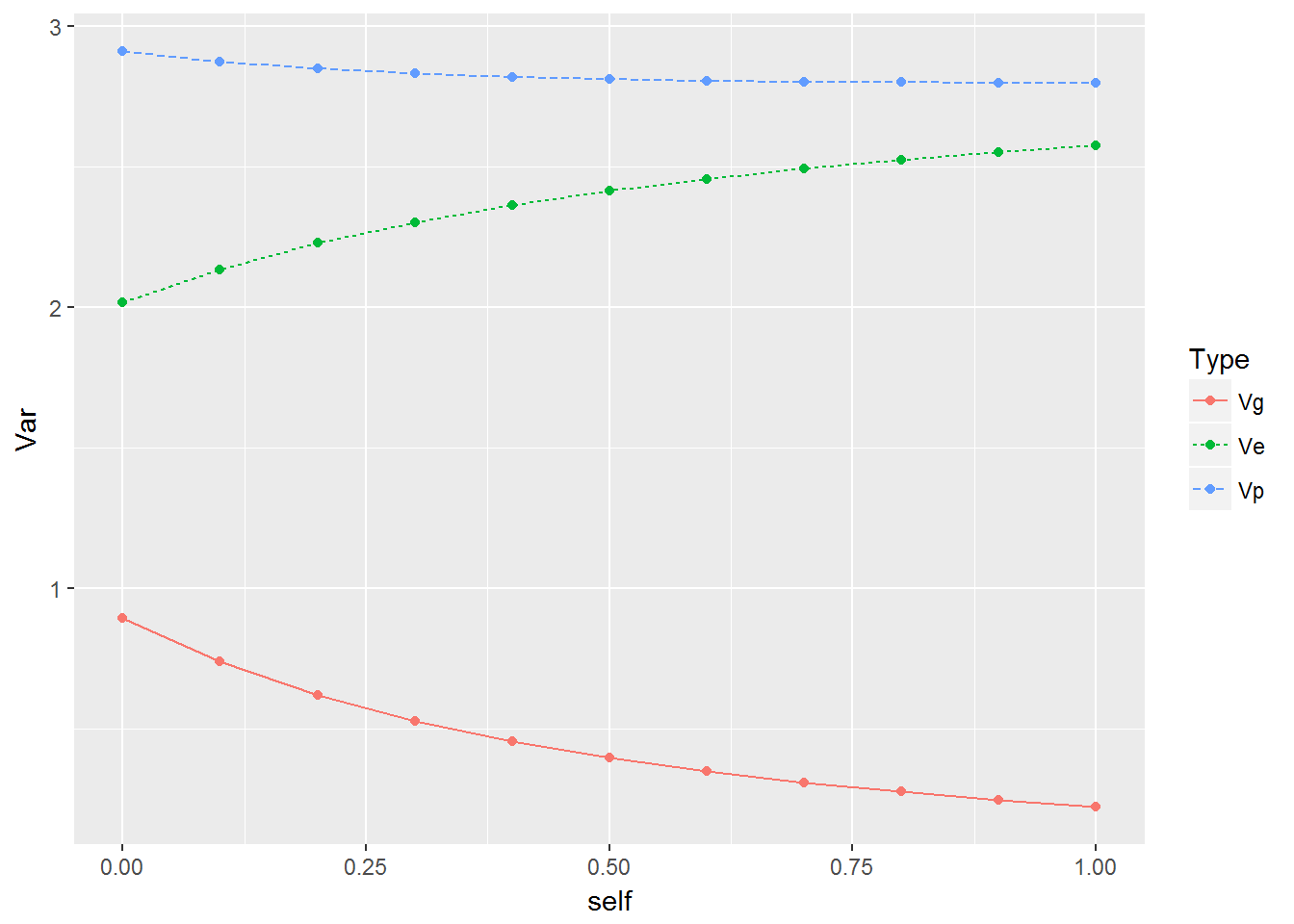
## self Vg Ve Vp
## 1 0.0 0.894 2.018 2.911
## 2 0.1 0.739 2.136 2.875
## 3 0.2 0.621 2.229 2.849
## 4 0.3 0.529 2.303 2.832
## 5 0.4 0.456 2.364 2.820
## 6 0.5 0.397 2.415 2.812
## 7 0.6 0.349 2.458 2.807
## 8 0.7 0.309 2.494 2.803
## 9 0.8 0.276 2.525 2.801
## 10 0.9 0.248 2.553 2.800
## 11 1.0 0.223 2.576 2.800
|
其中,Vg代表遗传方差,Ve代表误差方差,Vp代表表型方差。
由于近亲繁殖,部分自交群体的观测方差不止代表了非自交参考群体中的加性方差。因此,当自交率增加时,非自交参考群体中的遗传方差估计减少,而误差方差增大,但表型方差总体趋于稳定。
可以将上述结果图形化,以观测三者的变化趋势:
参考文献
- 林元震主编.《R与ASReml-R统计学》.中国林业出版社.2016
- Fikret Isik, et al. Genetic data analysis for plant and animal breeding. Springer 2017

