Yuanzhen Lin
菜单
置顶

用R进行G×E互作的AMMI模型分析

在多地点试验中，突出的一个问题是林木基因型与环境之间往往存在显著的交互作用(Genotype by environment interaction, GEI)，因此如何准确评估GEI对于后续林木良种的选育和推广至关重要。目前，农业上大多使用联合回归法1、主效可加互作可乘模型(Additive main effects multiplicative interaction, AMMI)2和基因型主效加基因型-环境互作效应双标图(Genotype Main Effect plus Genotype-by-Environment Interaction biplot, GGE双标图) 3分析多点试验，并据此来进行品种评价、试验点评价和品种生态区划分，其中GGE双标图越来越受关注。迄今，GGE双标图在林木上的应用4仍然很少，仅在少数树种如辐射松、杨树和乐昌含笑中有过报道。

00 示例数据集

示例采用agricolae包的数据集plrv。

1
2
3
4

    data(plrv,package='agricolae')

    names(plrv)
    str(plrv)

01 使用AMMI()建模

使用agricolae包的AMMI()建模，具体代码如下：

1
2

    model<- with(plrv,AMMI(ENV=Locality,GEN=Genotype,REP=Rep,
                               Y=Yield,console=F,PC=T))

现在可查看方差分析结果与GEI部分的主成分结果如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

    model$ANOVA # for aov
## Analysis of Variance Table
## 
## Response: Y
##            Df Sum Sq Mean Sq  F value    Pr(>F)    
## ENV         5 122284 24456.9 257.0382  9.08e-12 ***
## REP(ENV)   12   1142    95.1   2.5694  0.002889 ** 
## GEN        27  17533   649.4  17.5359 < 2.2e-16 ***
## ENV:GEN   135  23762   176.0   4.7531 < 2.2e-16 ***
## Residuals 324  11998    37.0                       
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
    
    model$analysis # for pc
##     percent  acum Df     Sum.Sq   Mean.Sq F.value   Pr.F
## PC1    56.3  56.3 31 13368.5954 431.24501   11.65 0.0000
## PC2    27.1  83.3 29  6427.5799 221.64069    5.99 0.0000
## PC3     9.4  92.7 27  2241.9398  83.03481    2.24 0.0005
## PC4     4.3  97.1 25  1027.5785  41.10314    1.11 0.3286
## PC5     2.9 100.0 23   696.1012  30.26527    0.82 0.7059

如果只保留前2个主成分，则可通过自编函数来操作：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

    # only keep the first two PCs
    PC.res <- function(model) {
      maov<-model$ANOVA # for aov
      df.res<-maov['Residuals','Df'] # residual df
      MS.res<-maov['Residuals','Mean Sq']
      
      cat('GEI aov results:\n')
      print(maov['ENV:GEN',])
      cat('\n\n')
      
      GEI<-model$analysis # for pc
      row.names(GEI)
      nr<-nrow(GEI)
      for(i in 1:7) GEI[nr+1,i]<-sum(GEI[3:nr,i])
      row.names(GEI)[nr+1]<-'PCres'
      
      GEI['PCres','acum']=GEI[nr,'acum']
      GEI['PCres','Mean.Sq']=round(GEI['PCres','Sum.Sq']/GEI['PCres','Df'],4)
      GEI['PCres','F.value']=round(GEI['PCres','Mean.Sq']/MS.res,4)
      GEI['PCres','Pr.F']=round(pf(GEI['PCres','F.value'], GEI['PCres','Df'], df.res,lower.tail=F),4)
      GEI$GEIp<-round(100*GEI$Sum.Sq/sum(GEI$Sum.Sq[1:nr]),4)

      
      for(i in c(1,3:4,8)) GEI[nr+2,i]<-sum(GEI[1:nr,i])
      row.names(GEI)[nr+2]<-'PCtl'
      GEI['PCtl','Mean.Sq']=round(GEI['PCtl','Sum.Sq']/GEI['PCtl','Df'],4)
      GEI['PCtl','F.value']=round(GEI['PCtl','Mean.Sq']/MS.res,4)
      
      return(GEI)
    }
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

    PCs.aov<-PC.res(model) # for GEI aov
    PCs.aov
##       percent  acum  Df     Sum.Sq   Mean.Sq F.value   Pr.F     GEIp
## PC1      56.3  56.3  31 13368.5954 431.24501 11.6500 0.0000  56.2609
## PC2      27.1  83.3  29  6427.5799 221.64069  5.9900 0.0000  27.0501
## PC3       9.4  92.7  27  2241.9398  83.03481  2.2400 0.0005   9.4351
## PC4       4.3  97.1  25  1027.5785  41.10314  1.1100 0.3286   4.3245
## PC5       2.9 100.0  23   696.1012  30.26527  0.8200 0.7059   2.9295
## PCres    16.6 100.0  75  3965.6195  52.87490  1.4278 0.0192  16.6891
## PCtl    100.0    NA 135 23761.7949 176.01330  4.7531     NA 100.0001

查看ASV和YSI结果：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

    (Idx2<-index.AMMI(model)) # for ASV
##           ASV YSI rASV rYSI    means
## G1  2.5131813  42   19   23 26.31947
## G10 1.1739456  28    6   22 26.34039
## G11 2.4615460  32   18   14 30.58975
## G12 2.0368354  29   11   18 28.17335
## G13 1.5167528  18    9    9 35.32583
## G14 4.8741897  30   27    3 38.75767
## G15 2.3623790  37   16   21 26.34808
## G16 2.0954103  36   12   24 26.01336
## G17 3.6050812  51   26   25 23.84175
## G18 2.3436592  23   15    8 36.11581
## G19 0.5966506  13    3   10 34.05974
## G2  1.3792025  21    8   13 31.28887
## G20 0.2026430  20    1   19 27.47748
## G21 2.7709324  36   20   16 28.98663
## G22 2.1722949  26   14   12 32.68323
## G23 0.9507170  11    4    7 36.19020
## G24 2.3663500  23   17    6 36.19602
## G25 0.5646275  13    2   11 33.26623
## G26 2.1652861  33   13   20 27.00126
## G27 5.5374138  56   28   28 16.15569
## G28 3.3470545  27   25    2 39.10400
## G3  1.7912464  25   10   15 30.10174
## G4  3.1531170  24   23    1 39.75624
## G5  2.8907699  26   21    5 36.95181
## G6  3.0764673  49   22   27 21.41747
## G7  1.2740344  33    7   26 22.98480
## G8  1.0521529  22    5   17 28.66655
## G9  3.3065468  28   24    4 38.63477

查看各基因型的PCs得分：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

    head(model$biplot[,1:5],8)
##     type    Yield       PC1          PC2        PC3
## G1   GEN 26.31947 -1.508289 -1.258765244  0.1922031
## G10  GEN 26.34039 -0.799485 -0.220768053  0.9853880
## G11  GEN 30.58975 -1.495438  1.186549449 -0.9255252
## G12  GEN 28.17335  1.393354  0.332786322  0.7322688
## G13  GEN 35.32583  1.051708 -0.002555823  0.8156191
## G14  GEN 38.75767  3.083381 -1.995946966 -0.8797167
## G15  GEN 26.34808 -1.557371 -0.732314249  0.4143257
## G16  GEN 26.01336 -1.358809  0.741980068 -0.8748011

02 结果可视化

可以使用plot()和AMMI.contour()来生成双标图：

1
2

    plot(model)
    AMMI.contour(model,distance=0.7,shape=8,col="red",lwd=2,lty=5)

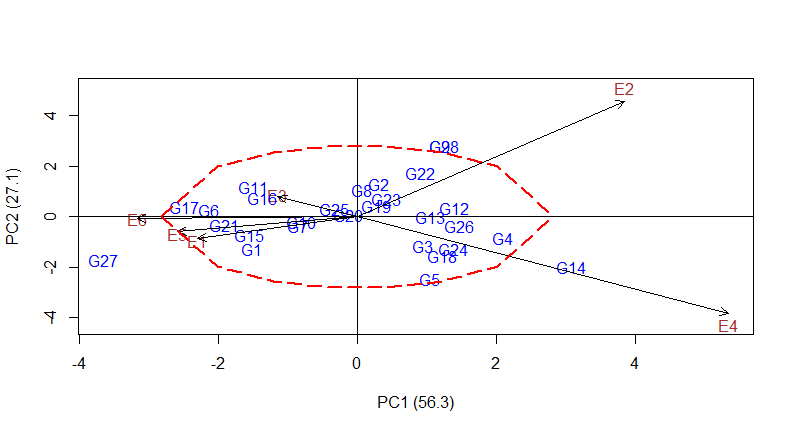
AMMI模型的双标图

图1 AMMI模型的双标图

对于GEI的结果可视化，不如GGE方法来得直观。后一篇博文将介绍如何使用R来可视化GGE方法。

03 方法局限性

3.1 AMMI 模型的局限性

  • 只限定于固定效应模型；
  • 假定各地点误差同质；
  • 要求数据是平衡的。

3.2 AMMI 模型可视化的局限性

  • 未能充分展示基因型的稳定性和高产性；
  • 未能充分展示试验地点间的关系。

04 参考文献

  1. Finlay K W, Wilkinson G N. The analysis of adaptation in a plant breeding programme [J]. Aust J Agric Res, 1963, 14: 742-754 [return]
  2. Gauch H G, Zobel R W. Identifying mega-environments and targeting genotypes [J]. Crop Sci, 1997, 37: 311-326 [return]
  3. Yan W. GGEbiplot—a Windows application for graphical analysis of multi-environment trial data and other types of two-way data [J]. Agron J, 2001, 93:1111-1118 [return]
  4. 程玲,张心菲, 张鑫鑫,等. 基于BLUP和GGE双标图的林木多地点试验分析[J]. 西北农林科技大学学报(自然科学版), 2018,46(3):87-93 [return]